TIL 230209 최대공약수와 최소공배수 with Python

알고리즘을 풀 때 자주 최대공약수가 필요한 경우가 생겼다.

 

최대공약수를 사용해 풀었던 문제

• 프로그래머스 레벨 0 / 분수의 덧셈
• 프로그래머스 레벨 0 / 유한소수 판별하기
• 프로그래머스 레벨 1 / 최대공약수와 최소공배수

여러 번 최대공약수를 구해야 하는 문제를 풀었는데도 매번 기억이 안 나서 까먹을 때마다 보려고 기록해 둔다.

 

 

최대공약수

유클리드 호제법

최대공약수는 유클리드 호제법을 이용하면 구할 수 있다.

두 개의 숫자가 있을 때 x를 y로 나누었을 때 나머지(r)가 0이면 y는 이 두 수의 최소공배수가 된다. 나머지가 0이 될 때까지 값을 앞으로 당겨가며 계속 반복하면 된다.

유클리드 호제법

 

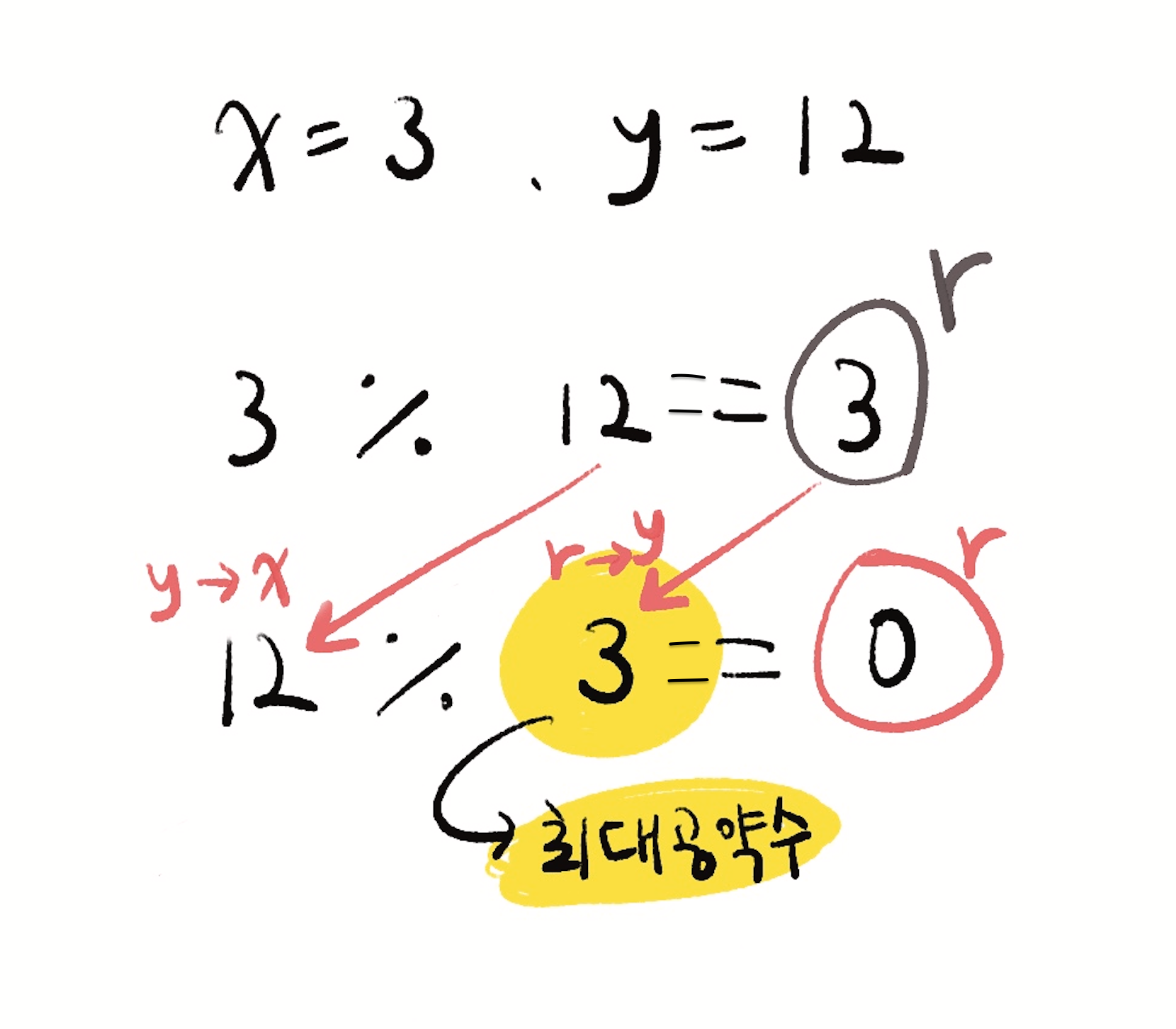
while문을 사용해서 표현했을 때 최소공배수가 구해진 시점(r이 0일때)에 y가 r이 되면 0이 되므로 종료된다. 하지만 그 윗줄이 이미 실행되어서 y는 x가 되었기 때문에 y가 아닌 x를 리턴한다.

def gcdWhile(x, y):
  r
  while y > 0:
    r = x % y
    x = y
    y = r
  return x

 

while문을 사용한 유클리드 호제법

 

python swap

파이썬은 swap이라는 문법이 있어서 위에서 r과 같이 값을 옮기기 위한 변수를 사용하지 않고 바로 바꿀 수 있다.

a, b = b, a

 

swap을 사용하면 더 간단히 표현할 수 있다.

def gcdWhile(x, y):
    while y > 0:
      x, y = y, x % y
    return x

 

최소공배수

최소공배수는 최대공약수를 구했다면 쉽게 구할 수 있다. 두 수의 곱을 최대공약수로 나눈 값이 최소공배수이다.

/를 사용하면 소수점까지 나와서 //를 사용하거나 int로 변환해 주었다.

def lcm(x, y):
	return x * y // gcd(x, y)

def lcm(x, y):
	return int(x * y / gcd(x, y))

 

math 라이브러리

하지만 놀랍게도 math 라이브러리를 사용하면 최대공약수와 최대공배수를 아주 간단하게 구할 수 있다.

gcd는 파이썬 버전 3.5부터 사용할 수 있다. (3.9버전부터는 인자를 3개 이상 받을 수 있다고 한다.)

lcm은 파이썬 버전 3.9부터 사용할 수 있다.

프로그래머스 최대공약수와 최소공배수 문제를 풀 때는 gcd만 사용가능했다.

import math
def solution(x, y):
  return [math.gcd(x,y), math.lcm(x,y)]